logicgerma.blogg.se - Gaussview 6 point group symmetry

#Gaussview 6 point group symmetry generator

Symmetrize a structure to a specific point group (raising or lowering its symmetry).

Add an atom at the centroid position of a selected group of atoms.

Flip the symmetry of a molecule by mirroring or inverting about a selected atom.

Changes can be isolated to the desired atom, group or fragment as required.

Examine and modify any structural parameter.

Save commonly-used fragments of your own to a custom library.

Easily build molecules using a wide range of pre-optimized groups, rings, amino acids and DNA bases.

Thus the classification of the finite subgroups of I( R 2) is up to conjugacy in I( R 2).GaussView provides powerful molecule building features, the most important of which are listed below. Similarly any two copies of the same dihedral group are also conjugate. That is, for some element g ∈ I( R 2) we have g G 1 g -1 = G 2. In fact (See Exercises 4 Question 1) any two copies G 1 and G 2 of the groups C n of rotations are conjugate in I( R 2).

#Gaussview 6 point group symmetry generator

If G ≠ H then H has two cosets in G (since SO(2) has two cosets in O(2)) and the reflections form a coset rH and it is easy to verify that if h is a generator of H then rhr = h -1. All the others must be multiples of this one (otherwise one could combine them to get a rotation whose magnitude was their hcf) and so we have H ≅ C n. H = G ∩ SO(2) contains only rotations and hence contains a smallest (non-zero) rotation. Take this point as the origin and then G ⊆ O(2). Hence there is a point of R 2 left fixed by all the elements of G. It can only contain reflections in lines through a common point (Otherwise one could combine two of them to get a rotation about one of the meeting points and a reflection through a different point). If it contains a rotation about a point a, it cannot contain a reflection in any line not through a (See Exercises 3 Question 2). It cannot contain rotations about two distinct points otherwise (See Exercises 3 Question 6) it would contain a translation. Then G cannot contain a translation or glide reflection since these elements have infinite orders.

The above examples C n and D n for some positive integer n are the only finite subgroups of I( R 2). Note that for each point p of R 2 there is a subgroup in I( R 2) isomorphic to C n and many subgroups isomorphic to D n (corresponding to the different directions that one could choose for the mirrors through p).

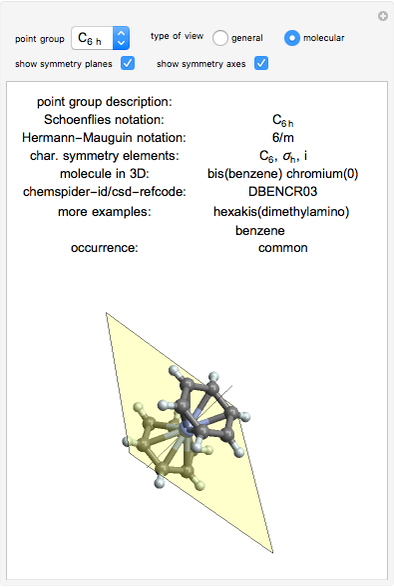
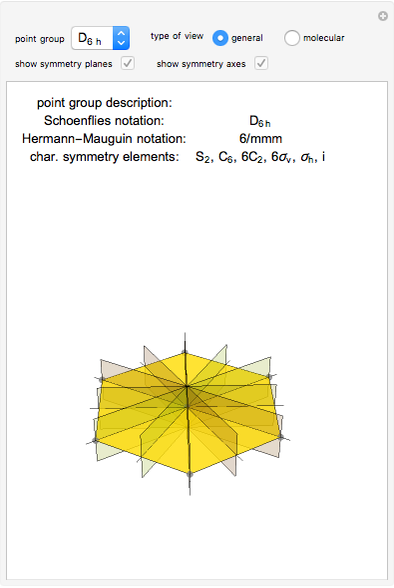
Note that as a group this is a cycle group of order 2 but that it is not the same subgroup as any of the subgroups C 2 of (1) above which are generated by rotations. The group D 1 is the group consisting of the identity and reflection in a line: It is sometimes written V and is isomorphic to C 2× C 2. The group D 2 is the symmetry group of a "regular 2-gon" and consists of the identity, rotation by π and reflections in two perpendicular lines. The group D 3 ≅ S 3 (the symmetric group on three symbols). One may show that in terms of generators and relations, D n=. The group D 4 consists of four rotations by multiples of π/2 and four reflections - two through lines joining vertices and two through lines joining mid-points of sides. The group D 3 consists of rotations by 0, 2π/3 and 4π/3 and three reflections. The Dihedral group D n is the group of symmetries of a regular n-gon. Has symmetry group C 2, has symmetry group C 3, has symmetry group C 4, etc. Note that C n is the symmetry group of many figures in R 2. Rotation by 2 π/ n generates a subgroup isomorphic to C n the cyclic group of order n. The subgroup is then the symmetry group of the subset X. In particular we look for subsets X of S = R 2 which are mapped to themselves by all the elements of these subgroups. We now consider some interesting subgroups of I( R 2).įollowing the spirit of Klein's Erlangen program we look for properties preserved by these subgroups. Symmetry groups of plane figures Course MT3818 Topics in Geometry